[ad_1]
Elementary particles in three dimensions are both bosons or fermions. The existence of solely two sorts is rooted in the truth that the worldlines of two particles in three plus one dimensions can all the time be untied in a trivial method. Therefore, exchanging a pair of indistinguishable particles twice is topologically equal to not exchanging them in any respect, and the wavefunction should stay the identical. Representing the change as a matrix R appearing on the area of wavefunctions with a continuing variety of particles, it’s thus required that R2 = 1 (a scalar), leaving two prospects: R = 1 (bosons) and R = −1 (fermions). Such steady deformation isn’t attainable in two dimensions, thus permitting collective excitations (quasiparticles) to point out richer braiding behaviour. Specifically, this allows the existence of Abelian anyons2,3,6,7,8,24,25, by which the worldwide part change as a result of braiding can take any worth. It has been proposed that there exists one other class of quasiparticles often known as non-Abelian anyons, by which braiding as a substitute ends in a change of the observables of the wavefunction4,5,24. In different phrases, R2 doesn’t simplify to a scalar, however stays a unitary matrix. Subsequently, R2 is a basic attribute of anyon braiding. The topological strategy to quantum computation26 goals to leverage these non-Abelian anyons and their topological nature to allow gate operations which are protected towards native perturbations and decoherence errors5,27,28,29,30. In solid-state methods, main candidates of non-Abelian quasiparticles are low-energy excitations in Hamiltonian methods, together with the 5/2 fractional quantum Corridor states31,32, vortices in topological superconductors33,34 and Majorana zero modes in semiconductors proximitized by superconductors35,36,37,38. Nevertheless, direct verification of non-Abelian change statistics has remained elusive39,40,41.
We formulate the required necessities for experimentally certifying a bodily system as a platform for topological quantum computation5,26: (1) create an anyon pair; (2) confirm the principles that govern the ‘collision’ of two anyons, often known as the fusion guidelines; (3) confirm the non-Abelian braiding statistics mirrored within the matrix construction R2 and (4) understand managed entanglement of anyonic levels of freedom. Notably, the statement of steps (2)–(4) requires measurements of multi-anyon states, by the use of fusion or non-local measurements.
The arrival of quantum processors permits for managed unitary evolution and direct entry to the wavefunction relatively than the parameters of the Hamiltonian. These options allow the usage of native operations for environment friendly preparation of topological states that may host non-Abelian anyons, and—as we are going to show—their subsequent braiding and fusion. Furthermore, these platforms enable for probing arbitrary Pauli strings by way of damaging multiqubit (that’s, non-local) measurements. Because the braiding of non-Abelian anyons on this platform is achieved by way of unitary gate management relatively than adiabatic evolution of a Hamiltonian system, we observe that the anyons aren’t quasiparticles within the sense of eigenstates that persist all through a Hamiltonian evolution. Their motion is achieved by way of native operations alongside their paths, and they’re stored spatially separated all through the braiding. We subsequently emphasize that the two-dimensional braiding processes are bodily going down on the system, resulting in precise non-Abelian change results of native anyons within the many-body wavefunction, relatively than matrix operations that merely observe the identical algebra.
To understand a many-body quantum state that may host anyons, it’s important to regulate the topological degeneracy. An appropriate platform for attaining this requirement is a stabilizer code42, by which the wavefunctions are characterised by a set of commuting operators ({{hat{S}}_{p}}) referred to as stabilizers, with ({hat{S}}_{p}left|psi rightrangle ={s}_{p}left|psi rightrangle ) and sp = ±1. The code area is the set of degenerate wavefunctions for which sp = 1 for all p. Therefore, each impartial stabilizer divides the degeneracy of the code area by two.
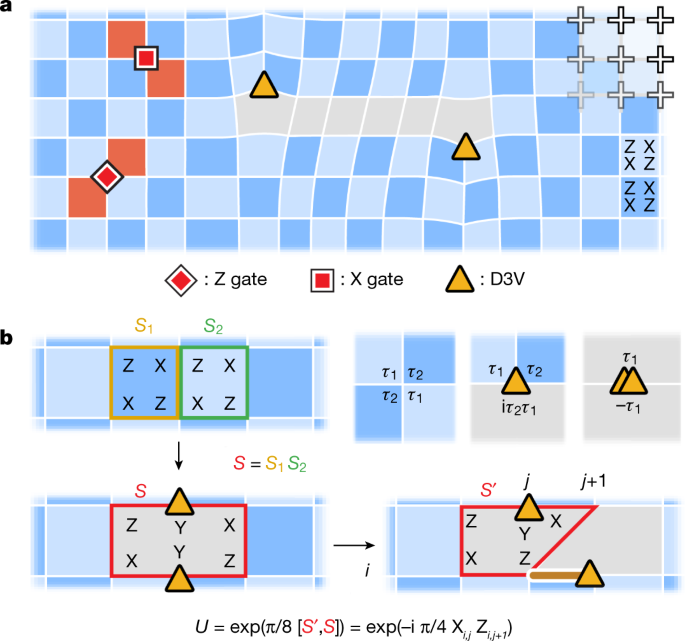
Whereas the bodily format of qubits is often used to find out the construction of the stabilizers, the qubits could be thought of to be diploma j vertices (DjV; j ∈ {2, 3, 4}) on extra common planar graphs (Fig. 1a)23. Utilizing this image, every stabilizer could be related to a plaquette p, whose vertices are the qubits on which ({hat{S}}_{p}) acts:
$${hat{S}}_{p}=prod _{v,in ,{rm{vertices}}}{hat{tau }}_{p,v}.$$
(1)
({hat{tau }}_{p,v}) is right here a single-qubit Pauli operator appearing on vertex v, chosen to fulfill a constraint round that vertex (Fig. 1b). An occasion the place sp = −1 on a plaquette known as a plaquette violation. These could be regarded as quasiparticles, that are created and moved by way of single-qubit Pauli operators (Fig. 1a). A pair of plaquette violations sharing an edge represent a fermion, ε. We not too long ago demonstrated the Abelian statistics of such quasiparticles within the floor code43. To understand non-Abelian statistics, one must transcend such plaquette violations; it has been proposed that dislocations within the stabilizer graph—analogous to lattice defects in crystalline solids—can host projective non-Abelian Ising anyons9,10. For brevity, we refer to those as ‘non-Abelian anyons’ or just ‘anyons’ from right here on.
a, Stabilizer codes are conveniently described in a graph framework. By means of deformations of the floor code graph, a sq. grid of qubits (crosses) can be utilized to understand extra generalized graphs. Plaquette violations (pink) correspond to stabilizers with sp = −1 and are created by native Pauli operations. Within the absence of deformations, plaquette violations are constrained to maneuver on one of many two sublattices of the twin graph within the floor code, therefore the 2 shades of blue. b, A pair of D3Vs (yellow triangles) seems by eradicating an edge between two neighbouring stabilizers, ({hat{S}}_{1}) and ({hat{S}}_{2}), and introducing the brand new stabilizer, (hat{S}={hat{S}}_{1}{hat{S}}_{2}). A D3V is moved by making use of a two-qubit entangling gate, (exp left(frac{pi }{8}[{hat{S}}^{{prime} },hat{S}]proper)). Within the presence of bulk D3Vs, there isn’t a constant approach of chequerboard colouring, therefore the (arbitrarily chosen) gray areas. The highest proper reveals that in a common stabilizer graph, ({hat{S}}_{p}) could be discovered from a constraint at every vertex, the place {τ1, τ2} = 0.
Within the graph framework launched above, it has been proven that such dislocations are characterised as vertices of diploma 2 and three (ref. 23). Contemplate the stabilizer graph of the floor code26,44, particularly with boundary circumstances such that the degeneracy is 2. Though all of the vertices within the bulk are D4Vs, one can create two D3Vs by eradicating an edge between two neighbouring plaquettes p and q, and introducing the brand new stabilizer (hat{S}={hat{S}}_{p}{hat{S}}_{q}) (Fig. 1b). Evidently, the introduction of two D3Vs reduces the variety of impartial stabilizers by one and thus doubles the degeneracy. This doubling is precisely what is anticipated when a pair of Ising anyons is launched9,10; therefore, D3Vs seem as a candidate of non-Abelian anyons, and we are going to denote them as σ.
To be braided and fused by unitary operations, the D3Vs have to be moved. Whereas the construction of the stabilizer graph is normally thought of to be static, it was predicted by Bombin that the dislocations within the floor code would present projective non-Abelian Ising statistics if braided10. Right here, we are going to use a particular protocol not too long ago proposed by Lensky et al.23 for deforming the stabilizer graph (and thus transferring the anyons) utilizing native two-qubit Clifford gates. To shift a D3V from vertex u to v, an edge have to be disconnected from v and reconnected to u. This may be achieved by the use of the gate unitary (exp left(frac{pi }{8}[{hat{S}}_{p}^{{prime} },{hat{S}}_{p}]proper)), the place ({hat{S}}_{p}) is the unique stabilizer containing the sting and u, and ({hat{S}}_{p}^{{prime} }) is the brand new stabilizer that emerges after transferring the sting23. In instances the place the D3V is shifted between two related vertices, the unitary simplifies to the shape ({U}_{pm }({hat{tau }}_{u}{hat{tau }}_{v})equiv exp left(pm ifrac{pi }{4}{hat{tau }}_{u}{hat{tau }}_{v}proper)), the place ({hat{tau }}_{u}) and ({hat{tau }}_{v}) are Pauli operators appearing on vertices u and v. We experimentally understand this unitary by way of a managed Z (CZ) gate and single-qubit rotations (median errors of seven.3 × 10−3 and 1.3 × 10−3, respectively; Strategies).
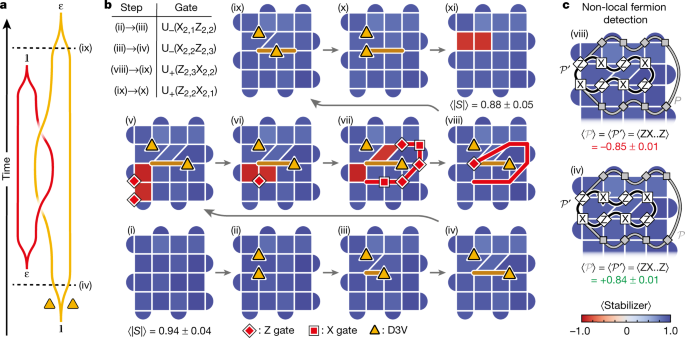
Following these insights from Kitaev and Bombin, we now flip to our experimental research of the proposed anyons, utilizing the protocol described in ref. 23. Within the first experiment, we show the creation of anyons and the basic fusion guidelines of σ and ε (Fig. 2a). In a 5 × 5 grid of superconducting qubits, we first use a protocol consisting of 4 layers of CZ gates to arrange the floor code floor state (Fig. 2b(i), see additionally ref. 43). The typical stabilizer worth after the bottom state preparation is 0.94 ± 0.04 (particular person stabilizer values proven in Prolonged Information Fig. 3c). We then take away a stabilizer edge to create a pair of D3Vs (σ) and separate them by way of the applying of two-qubit gates. Fig. 2b(i)–(iv) present the measured stabilizer values within the resultant graph in every step of this process (decided by concurrently measuring the concerned qubits of their respective bases, n = 10,000; observe that the measurements are damaging and the protocol is restarted after every measurement). In Fig. 2b(v), single-qubit Z gates are utilized to 2 qubits close to the decrease left nook of the grid to create adjoining plaquette violations, which collectively type a fermion. By means of the sequential software of X and Z gates (Fig. 2b(vii)–(viii)), one of many plaquette violations is then made to encircle the best σ vertex. Crucially, after transferring round σ, the plaquette violation doesn’t return to the place it began, however relatively to the situation of the opposite plaquette violation. This permits them to annihilate (Fig. 2b(viii)), inflicting the fermion to seemingly disappear. Nevertheless, by bringing the 2 σ again collectively and annihilating them (Fig. 2b(ix)–(xi)), we arrive at a placing statement: an ε particle re-emerges on two of the sq. plaquettes the place the σ vertices beforehand resided.
a, The braiding worldlines used to fuse ε and σ. b, Expectation values of stabilizers at every step of the unitary operation after readout correction (see Prolonged Information Fig. 3 for particulars and particular person stabilizer values). We first put together the bottom state of the floor code (step (i); common stabilizer worth of 0.94 ± 0.04, the place the uncertainty is one commonplace deviation). A D3V (σ) pair is then created (ii) and separated (iii)–(iv), earlier than making a fermion, ε (v). One of many plaquette violations is introduced round the best σ (vi)–(viii), permitting it to annihilate with the opposite plaquette violation (viii). The fermion has seemingly disappeared, however re-emerges when the σ are annihilated ((xi); stabilizer values −0.86 and −0.87). The trail (v) → (viii) demonstrates the fusion rule, σ × ε = σ. The totally different fermion parities on the finish of the paths (viii) → (xi) and (iv) → (i) present the opposite fusion rule, (sigma instances sigma ={mathbb{1}}+varepsilon ). Yellow triangles characterize the positions of the σ. The brown and pink strains denote the paths of the σ and the plaquette violation, respectively. Purple squares (diamonds) characterize X (Z) gates. Higher left reveals a desk of two-qubit unitaries used within the protocol. Every stabilizer was measured n = 10,000 instances in every step. c, A non-local method for hidden fermion detection: the presence of a fermion in a σ-pair could be deduced by measuring the signal of the Pauli string (hat{{mathcal{P}}}) equivalent to bringing a plaquette violation across the σ-pair (gray path). (hat{{mathcal{P}}}) is equal to the shorter string (hat{{{mathcal{P}}}^{{prime} }}) (black path). Measurements of (hat{{{mathcal{P}}}^{{prime} }}) in steps (viii) (high) and (iv) (backside) give values of −0.85 ± 0.01 and +0.84 ± 0.01, respectively. This means that there’s a hidden fermion pair within the former case, however not within the latter, regardless of the stabilizers being the identical.
Our outcomes show the fusion of ε and σ. The disappearance of the fermion from step (v) to (viii) establishes the basic fusion rule of ε and σ:
$$sigma instances varepsilon =sigma .$$
(2)
We emphasize that not one of the single-qubit gates alongside the trail of the plaquette violation are utilized to the qubits internet hosting the cell σ; our observations are subsequently solely because of the non-local results of non-Abelian D3Vs, and exemplify the unconventional behaviour of the latter. Furthermore, one other fusion rule is seen by contemplating the reverse path (iv) → (i), and evaluating it to the trail (viii) → (xi). These two paths show {that a} pair of σ can fuse to type both vacuum (({mathbb{1}})) or one fermion (steps (i) and (xi), respectively):
$$sigma instances sigma ={mathbb{1}}+varepsilon .$$
(3)
The beginning factors of those two paths ((iv) and (viii)) can’t be distinguished by any native measurement. We subsequently introduce a non-local measurement method that enables for detecting an ε with out fusing the σ (refs. 10,23,26). The important thing thought underlying this methodology is that bringing a plaquette violation round a fermion ought to lead to a π part. We subsequently measure the Pauli string (hat{{mathcal{P}}}) that corresponds to creating two plaquette violations, bringing one in all them across the two σ, and at last annihilating them with one another (gray paths in Fig. 2c). The existence of an ε contained in the σ-pair ought to trigger (langle hat{{mathcal{P}}}rangle =-1). To simplify this system additional, (hat{{mathcal{P}}}) could be lowered to a shorter string (hat{{{mathcal{P}}}^{{prime} }}) (black paths in Fig. 2c) by making the most of the stabilizers it encompasses. For example, if (hat{{mathcal{P}}}) accommodates three of the operators in a four-qubit stabilizer, these could be switched out with the remaining operator. Measuring (langle hat{{{mathcal{P}}}^{{prime} }}rangle ) in step (iv), by which the σ are separated however the fermion has not but been launched, offers (langle hat{{{mathcal{P}}}^{{prime} }}rangle =+,0.84pm 0.01), in line with the absence of fermions (Fig. 2c). Nevertheless, performing the very same measurement in step (viii), by which the σ are in the identical positions, we discover (langle hat{{{mathcal{P}}}^{{prime} }}rangle =-,0.85pm 0.01), indicating that an ε is delocalized throughout the spatially separated σ pair (Fig. 2c). This statement highlights the non-local encoding of the fermions, which can’t be defined with classical physics.
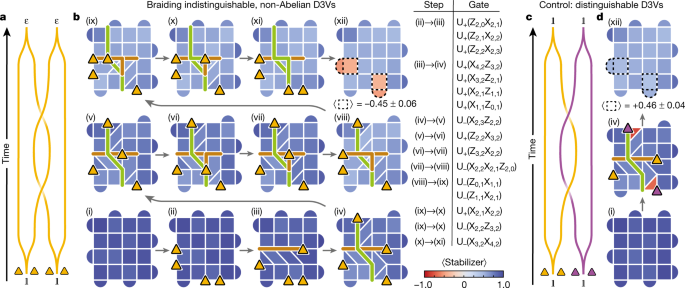
Having demonstrated the above fusion guidelines involving σ, we subsequent braid them with one another to instantly present their non-Abelian statistics. We take into account two spatially separated σ pairs, A and B, by eradicating two stabilizer edges (Fig. 3a,b(ii)). Subsequent, we apply two-qubit gates alongside a horizontal path to separate the σ in pair A (Fig. 3b(iii)), adopted by the same process within the vertical route on pair B (Fig. 3b(iv)), in order that one in all its σ crosses the trail of pair A. We then subsequently deliver the σ from pairs A and B again to their unique positions (Fig. 3b(v)–(viii) and (ix)–(xi), respectively). When the 2 σ pairs are annihilated within the ultimate step (Fig. 3b(xii)), we observe {that a} fermion is revealed in every of the positions the place the σ pairs resided (common stabilizer worth −0.45 ± 0.06). This reveals a transparent change in native observables from the preliminary state by which no fermions had been current. As a management experiment, we repeat the experiment with distinguishable σ pairs, achieved by attaching a plaquette violation to every of the σ in pair B (Fig. 3c,d; see additionally Prolonged Information Fig. 8 for stabilizer measurements by way of the total protocol). Shifting the plaquette violation together with the σ requires a string of single-qubit gates, which switches the route of the rotation within the multiqubit unitaries, U± → U∓. On this case, no fermions are noticed on the finish of the protocol (common stabilizer worth +0.46 ± 0.04), thus offering a profitable management.
a, Wordline schematic of the braiding course of. b, Experimental demonstration of braiding, exhibiting the values of the stabilizers all through the method. Two σ pairs, A and B, are created from the vacuum ({mathbb{1}}), and one of many σ in pair A is dropped at the best aspect of the grid. Subsequent, a σ from pair B is moved to the highest, thus crossing the trail of pair A, earlier than bringing σ pairs A and B again collectively to finish the braid. Within the ultimate step, two fermions seem within the areas the place the σ pairs resided, constituting a change within the native observables. The diagonal σ transfer in step (iv) requires two SWAP gates (three CZ gates every) and a complete of ten CZ gates. The three-qubit unitary in step (viii) requires 4 SWAP gates and a complete of 15 CZ gates. Within the full circuit, a complete of 40 layers of CZ gates are utilized (Strategies). The yellow triangles characterize the areas of the σ; the brown and inexperienced strains characterize the paths of σ from pairs A and B, respectively. The 4 pink stabilizers in (xii) have a imply worth of −0.45 ± 0.06, the place the uncertainty is one commonplace deviation. Every stabilizer was measured n = 10,000 instances in every step. c, As a management experiment, we carry out the identical braid as in a, however with distinguishable σ by attaching a plaquette violation to the σ in pair B (represented with purple triangles). d, Identical as b, however utilizing distinguishable σ (solely exhibiting steps (i), (iv) and (xii)). In distinction to b, no fermions are noticed in step (xii).
Fermions can solely be created in pairs within the bulk. Furthermore, the fusion of two σ can solely create zero or one fermion (equation (3)). Therefore, our experiment includes the minimal variety of bulk σ (4) wanted to encode two fermions and show non-Abelian braiding. As a result of the fermion parity is conserved, results of gate imperfections and decoherence could be partially mitigated by postselecting for an excellent variety of fermions. This ends in fermion detection values of −0.76 ± 0.03 and +0.79 ± 0.04 in Fig. 3b,d, respectively.
Collectively, our observations present the change in native observables by braiding of indistinguishable σ and represent a direct demonstration of their non-Abelian statistics. In different phrases, the double-braiding operation R2 is a matrix that can not be lowered to a scalar. Particularly, it corresponds to an X gate appearing on the area spanned by zero- and two-fermion wavefunctions.
The complete braiding circuit consists of 40 layers of CZ gates and 41 layers of single-qubit gates (36 of every after floor state preparation). The results of imperfections on this {hardware} implementation could be assessed by way of comparability with the management experiment. Absolutely the values of the stabilizers by which the fermions are detected within the two experiments (dashed containers in Fig. 3b,d(xii)) are very related (common values of −0.45 and +0.46). That is in line with the depolarization channel mannequin, by which the measured stabilizer values are proportional to the best values (±1).
We subsequent research the prospects of utilizing D3Vs to encode logical qubits and put together an entangled state of anyon pairs. By doubling the degeneracy, every extra σ pair introduces one logical qubit, the place the (0rightrangle _{{rm{L}}}) (( 1rangle _{{rm{L}}})) state corresponds to an excellent (odd) variety of hidden fermions. The measurements of the fermion numbers in a number of σ pairs aren’t absolutely impartial: bringing a plaquette violation round one σ pair is equal to bringing it round all the opposite pairs (because of the conservation of fermionic parity). Therefore, N ≥ 2 anyons encode N/2 − 1 logical qubits. The D3Vs we’ve got created and manipulated to this point aren’t the one ones current within the stabilizer graph; with the boundary circumstances used right here, every of the 4 corners are additionally D3Vs, no totally different from these within the bulk23. Certainly, the existence of D3Vs within the corners is the explanation why a single fermion might be created within the nook in Fig. 2b(v). That is additionally in line with the truth that the floor code itself encodes one logical qubit within the absence of extra D3Vs. Right here we create two pairs of D3Vs, along with the 4 which are already current within the corners, to encode a complete of three logical qubits.
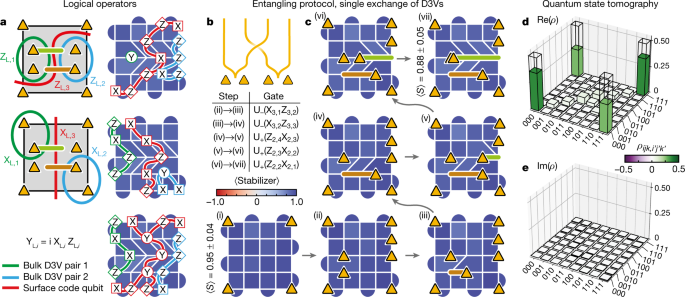
By means of the usage of braiding, we intention to arrange an entangled state of those logical qubits, particularly a GHZ state on the shape ((| 000rangle +| 111rangle )/sqrt{2}). The definition of a GHZ state and the specifics of how it’s ready is basis-dependent. In most methods, the levels of freedom are native and there’s a pure selection of foundation. For spatially separated anyons, the measurement operators are essentially non-local. Right here we select the premise outlined as follows: for the primary two logical qubits, we select the logical ({hat{Z}}_{{rm{L}},i}) operators to be Pauli strings encircling every of the majority σ pairs, as was utilized in Fig. 2c (inexperienced and turquoise paths within the left column of Fig. 4a). For the logical floor code qubit, we outline ({hat{Z}}_{{rm{L}},3}) because the Pauli string that crosses the grid horizontally by way of the hole between the majority D3V pairs, successfully enclosing 4 σ (pink path in Fig. 4a). On this foundation, the preliminary state is a product state.
a, Logical operators of the three logical qubits encoded within the eight anyons (different foundation decisions are attainable). The colored curves within the left column denote plaquette violation paths, earlier than discount to shorter, equal Pauli strings measured within the experiment (proper column). b, Worldline schematic of the one change used to understand an entangled state of the logical qubits. c, Single change of the non-Abelian anyons, exhibiting measurements of the stabilizers all through the protocol. Yellow triangles characterize the areas of the σ, whereas brown and inexperienced strains denote their paths. The typical stabilizer values are 0.95 ± 0.04 and 0.88 ± 0.05 (one commonplace deviation) within the first and final step, respectively. Every stabilizer was measured n = 20,000 instances in every step. d,e, Actual (d) and imaginary (e) elements of the reconstructed density matrix from the quantum state tomography. ({rm{Re}}(rho )) has clear peaks in its corners, as anticipated for a GHZ state on the shape ((left|000rightrangle +left|111rightrangle )/sqrt{2}). The overlap with the best GHZ state is ({rm{Tr}}{,{rho }_{{rm{GHZ}}}rho }=0.623pm 0.004), the place the uncertainty is one commonplace deviation decided from bootstrapping.
Whereas a double braid was used to implement the operator X in Fig. 3, we now carry out a single braid (Fig. 4b) to understand (sqrt{X}) and create a GHZ state. We implement this protocol by bringing one σ from every bulk pair throughout the grid to the opposite aspect (Fig. 4c). For each anyon double change throughout a Pauli string, the worth of the Pauli string modifications signal. Therefore, a double change would change (left|000rightrangle ) to (left|111rightrangle ), whereas a single change is anticipated to understand the superposition, ((left|111rightrangle +left|000rightrangle )/sqrt{2}).
To check the impact of this operation, we carry out quantum state tomography on the ultimate state, which requires measurements of not solely ({hat{Z}}_{{rm{L}},i}), but additionally ({hat{X}}_{{rm{L}},i}) and ({hat{Y}}_{{rm{L}},i}) on the three logical qubits. For the primary two logical qubits, ({hat{X}}_{{rm{L}},i}) is the Pauli string that corresponds to bringing a plaquette violation round solely one of many σ within the pair (as demonstrated in Fig. 2b). Each the logical ({hat{X}}_{{rm{L}},i}) and ({hat{Z}}_{{rm{L}},i}) operators could be simplified by lowering the unique Pauli strings (inexperienced and turquoise paths within the left column of Fig. 4c) to equal, shorter ones (proper column). ({hat{Z}}_{{rm{L}},1}) can in actual fact be lowered to a single (hat{Y})-operator. For the logical floor code qubit, we outline ({hat{X}}_{{rm{L}},3}) because the Pauli string that crosses the grid vertically between the majority D3V pairs (pink path in Fig. 4a). Lastly, the logical ({hat{Y}}_{{rm{L}},i})-operators are merely discovered from ({hat{Y}}_{{rm{L}},i}=i{hat{X}}_{{rm{L}},i}{hat{Z}}_{{rm{L}},i}). Measuring these operators, we reconstruct the density matrix of the ultimate state (Fig. 4d,e), which has a purity of (sqrt{{rm{Tr}}{{rho }^{2}}}=0.646pm 0.003) and an overlap with the best GHZ state of ({rm{Tr}}{{rho }_{{rm{GHZ}}}rho }=0.623pm 0.004) (uncertainties estimated from bootstrapping methodology; resampled 10,000 instances from the unique knowledge set). The truth that the state constancy is much like the purity means that the infidelity is nicely described by a depolarizing error channel.
In conclusion, we’ve got realized extremely controllable braiding of degree-3 vertices, enabling the demonstration of the fusion and braiding guidelines of non-Abelian Ising anyons. Now we have additionally proven that braiding can be utilized to create an entangled state of three logical qubits encoded in these anyons. In different, extra typical candidate platforms for non-Abelian change statistics, which contain Hamiltonian dynamics of quasi-particle excitations, topological safety naturally arises from an emergent hole that separates the computational states from different states. To leverage the non-Abelian anyons in our system for topologically protected quantum computing, the stabilizers have to be measured all through the braiding protocol. The potential inclusion of this error correction process, which includes overheads together with readout of five-qubit stabilizers, might open a brand new path in the direction of fault-tolerant implementation of Clifford gates, a key ingredient of common quantum computation.
[ad_2]